Properties that are common to all distributions are accessed via non-member getter functions: non-membership allows more of these functions to be added over time, as the need arises. Unfortunately the literature uses many different and confusing names to refer to a rather small number of actual concepts; refer to the concept index to find the property you want by the name you are most familiar with. Or use the function index to go straight to the function you want if you already know its name.

Function Index

Conceptual Index

Cumulative Distribution Function

template <class RealType, class Policy>
RealType cdf(const Distribution-Type<RealType, Policy>& dist, const RealType& x);

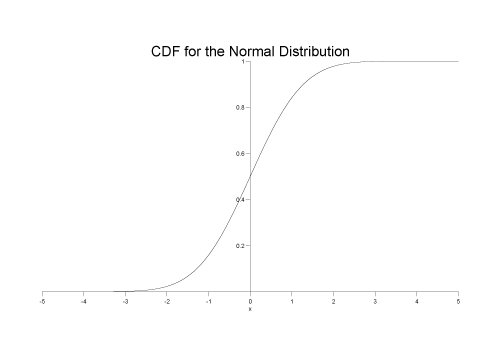
The Cumulative Distribution Function is the probability that the variable takes a value less than or equal to x. It is equivalent to the integral from -infinity to x of the Probability Density Function.

This function may return a domain_error if the random variable is outside the defined range for the distribution.

For example, the following graph shows the cdf for the normal distribution:

Complement of the Cumulative Distribution Function

template <class Distribution, class RealType>
RealType cdf(const Unspecified-Complement-Type<Distribution, RealType>& comp);

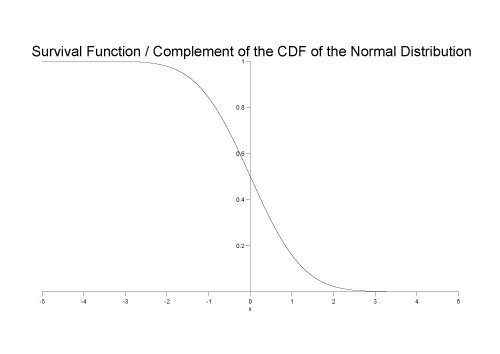
The complement of the Cumulative Distribution Function is the probability that the variable takes a value greater than x. It is equivalent to the integral from x to infinity of the Probability Density Function, or 1 minus the Cumulative Distribution Function of x.

This is also known as the survival function.

This function may return a domain_error if the random variable is outside the defined range for the distribution.

In this library, it is obtained by wrapping the arguments to the cdf function in a call to complement, for example:

// standard normal distribution object:
boost::math::normal norm;
// print survival function for x=2.0:
std::cout << cdf(complement(norm, 2.0)) << std::endl;

For example, the following graph shows the __complement of the cdf for the normal distribution:

See why complements? for why the complement is useful and when it should be used.

Hazard Function

template <class RealType, class Policy>
RealType hazard(const Distribution-Type<RealType, Policy>& dist, const RealType& x);

Returns the Hazard Function of x and distibution dist.

This function may return a domain_error if the random variable is outside the defined range for the distribution.

	Caution
	Some authors refer to this as the conditional failure density function rather than the hazard function.

Cumulative Hazard Function

template <class RealType, class Policy>
RealType chf(const Distribution-Type<RealType, Policy>& dist, const RealType& x);

Returns the Cumulative Hazard Function of x and distibution dist.

This function may return a domain_error if the random variable is outside the defined range for the distribution.

	Caution
	Some authors refer to this as simply the "Hazard Function".

mean

template<class RealType, class Policy>
RealType mean(const Distribution-Type<RealType, Policy>& dist);

Returns the mean of the distribution dist.

This function may return a domain_error if the distribution does not have a defined mean (for example the Cauchy distribution).

median

template<class RealType, class Policy>
RealType median(const Distribution-Type<RealType, Policy>& dist);

Returns the median of the distribution dist.

mode

template<class RealType, Policy>
RealType mode(const Distribution-Type<RealType, Policy>& dist);

Returns the mode of the distribution dist.

This function may return a domain_error if the distribution does not have a defined mode.

Probability Density Function

template <class RealType, class Policy>
RealType pdf(const Distribution-Type<RealType, Policy>& dist, const RealType& x);

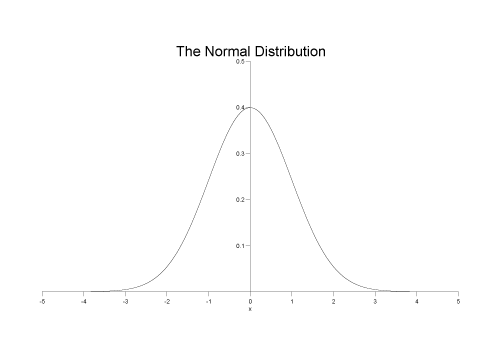
For a continuous function, the probability density function (pdf) returns the probability that the variate has the value x. Since for continuous distributions the probability at a single point is actually zero, the probability is better expressed as the integral of the pdf between two points: see the Cumulative Distribution Function.

For a discrete distribution, the pdf is the probability that the variate takes the value x.

This function may return a domain_error if the random variable is outside the defined range for the distribution.

For example, for a standard normal distribution the pdf looks like this:

Range

template<class RealType, class Policy>
std::pair<RealType, RealType> range(const Distribution-Type<RealType, Policy>& dist);

Returns the valid range of the random variable over distribution dist.

Quantile

template <class RealType, class Policy>
RealType quantile(const Distribution-Type<RealType, Policy>& dist, const RealType& p);

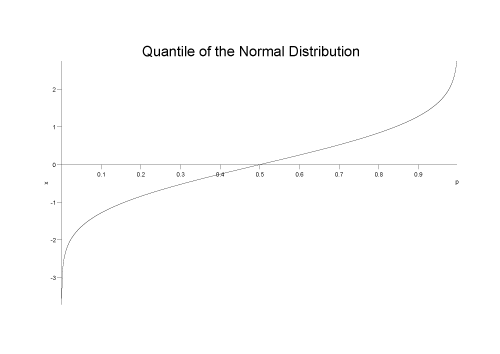
The quantile is best viewed as the inverse of the Cumulative Distribution Function, it returns a value x such that cdf(dist, x) == p.

This is also known as the percent point function, or percentile, or fractile, it is also the same as calculating the lower critical value of a distribution.

This function returns a domain_error if the probability lies outside [0,1]. The function may return an overflow_error if there is no finite value that has the specified probability.

The following graph shows the quantile function for a standard normal distribution:

Quantile from the complement of the probability.

See also complements.

template <class Distribution, class RealType>
RealType quantile(const Unspecified-Complement-Type<Distribution, RealType>& comp);

This is the inverse of the Complement of the Cumulative Distribution Function. It is calculated by wrapping the arguments in a call to the quantile function in a call to complement. For example:

// define a standard normal distribution:
boost::math::normal norm;
// print the value of x for which the complement
// of the probability is 0.05:
std::cout << quantile(complement(norm, 0.05)) << std::endl;

The function computes a value x such that cdf(complement(dist, x)) == q where q is complement of the probability.

Why complements?

This function is also called the inverse survival function, and is the same as calculating the upper critical value of a distribution.

This function returns a domain_error if the probablity lies outside [0,1]. The function may return an overflow_error if there is no finite value that has the specified probability.

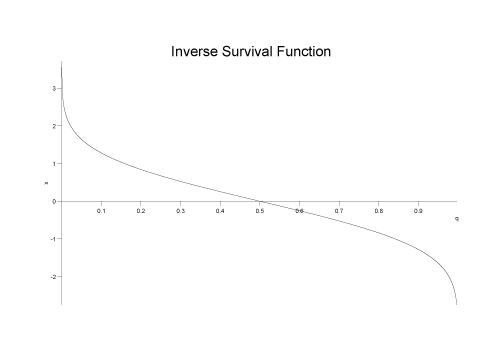
The following graph show the inverse survival function for the normal distribution:

Standard Deviation

template <class RealType, class Policy>
RealType standard_deviation(const Distribution-Type<RealType, Policy>& dist);

Returns the standard deviation of distribution dist.

This function may return a domain_error if the distribution does not have a defined standard deviation.

support

template<class RealType, class Policy>
std::pair<RealType, RealType> support(const Distribution-Type<RealType, Policy>& dist);

Returns the supported range of random variable over the distribution dist.

The distribution is said to be 'supported' over a range that is "the smallest closed set whose complement has probability zero". Non-mathematicians might say it means the 'interesting' smallest range of random variate x that has the cdf going from zero to unity. Outside are uninteresting zones where the pdf is zero, and the cdf zero or unity.

Variance

template <class RealType, class Policy>
RealType variance(const Distribution-Type<RealType, Policy>& dist);

Returns the variance of the distribution dist.

This function may return a domain_error if the distribution does not have a defined variance.

Skewness

template <class RealType, class Policy>
RealType skewness(const Distribution-Type<RealType, Policy>& dist);

Returns the skewness of the distribution dist.

This function may return a domain_error if the distribution does not have a defined skewness.

Kurtosis

template <class RealType, class Policy>
RealType kurtosis(const Distribution-Type<RealType, Policy>& dist);

Returns the 'proper' kurtosis (normalized fourth moment) of the distribution dist.

kertosis = β₂  = μ₄   / μ₂²

Where μ_i   is the i'th central moment of the distribution, and in particular μ₂   is the variance of the distribution.

The kurtosis is a measure of the "peakedness" of a distribution.

Note that the literature definition of kurtosis is confusing. The definition used here is that used by for example Wolfram MathWorld (that includes a table of formulae for kurtosis excess for various distributions) but NOT the definition of kurtosis used by Wikipedia which treats "kurtosis" and "kurtosis excess" as the same quantity.

kurtosis_excess = 'proper' kurtosis - 3

This subtraction of 3 is convenient so that the kurtosis excess of a normal distribution is zero.

This function may return a domain_error if the distribution does not have a defined kurtosis.

'Proper' kurtosis can have a value from zero to + infinity.

Kurtosis excess

template <class RealType, Policy>
RealType kurtosis_excess(const Distribution-Type<RealType, Policy>& dist);

Returns the kurtosis excess of the distribution dist.

kurtosis excess = γ₂  = μ₄   / μ₂²  - 3 = kurtosis - 3

Where μ_i   is the i'th central moment of the distribution, and in particular μ₂   is the variance of the distribution.

The kurtosis excess is a measure of the "peakedness" of a distribution, and is more widely used than the "kurtosis proper". It is defined so that the kurtosis excess of a normal distribution is zero.

This function may return a domain_error if the distribution does not have a defined kurtosis excess.

Kurtosis excess can have a value from -2 to + infinity.

kurtosis = kurtosis_excess +3;

The kurtosis excess of a normal distribution is zero.

P and Q

The terms P and Q are sometimes used to refer to the Cumulative Distribution Function and its complement respectively. Lowercase p and q are sometimes used to refer to the values returned by these functions.

Percent Point Function or Percentile

The percent point function, also known as the percentile, is the same as the Quantile.

Inverse CDF Function.

The inverse of the cumulative distribution function, is the same as the Quantile.

Inverse Survival Function.

The inverse of the survival function, is the same as computing the quantile from the complement of the probability.

Probability Mass Function

The Probability Mass Function is the same as the Probability Density Function.

The term Mass Function is usually applied to discrete distributions, while the term Probability Density Function applies to continuous distributions.

Lower Critical Value.

The lower critical value calculates the value of the random variable given the area under the left tail of the distribution. It is equivalent to calculating the Quantile.

Upper Critical Value.

The upper critical value calculates the value of the random variable given the area under the right tail of the distribution. It is equivalent to calculating the quantile from the complement of the probability.

Survival Function

Refer to the Complement of the Cumulative Distribution Function.