Octonions, like quaternions, are a relative of complex numbers.

Octonions see some use in theoretical physics.

In practical terms, an octonion is simply an octuple of real numbers (α,β,γ,δ,ε,ζ,η,θ), which we can write in the form o = α + βi + γj + δk + εe' + ζi' + ηj' + θk', where i, j and k are the same objects as for quaternions, and e', i', j' and k' are distinct objects which play essentially the same kind of role as i (or j or k).

Addition and a multiplication is defined on the set of octonions, which generalize their quaternionic counterparts. The main novelty this time is that the multiplication is not only not commutative, is now not even associative (i.e. there are octonions x, y and z such that x(yz) ≠ (xy)z). A way of remembering things is by using the following multiplication table:

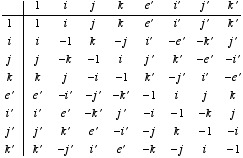
Octonions (and their kin) are described in far more details in this other document (with errata and addenda).

Some traditional constructs, such as the exponential, carry over without too much change into the realms of octonions, but other, such as taking a square root, do not (the fact that the exponential has a closed form is a result of the author, but the fact that the exponential exists at all for octonions is known since quite a long time ago).